Who is asking: Student
Level: Middle
Question:
Hi,
I'm really having trouble finding out the inverse of this quintic equation. F(X)= X5+3X3+1.I know that this quintic has an inverse because it is one to one. But I can't find a method to solve this. Finding the inverse of a quadratic or a cubic equation is a lot easier, but with this quintc I am really lost. I even know how the graph of this equation and its inverse looks like, but I'm not sure if Iam getting the right equation. Please help me out.
Thank you
Hi,
I can't do much more than you did. I plotted your function

f(x) = x5 + 3x3 + 1
and its inverse
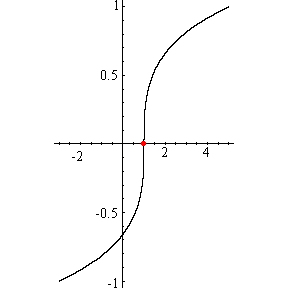
f-1(x)
I agree that the function is one-to-one so its inverse is also a function but I don't know how to write the inverse in a nice algebraic form. This is not surprising. It's easy to draw a curve that is the graph of a function and yet be unable to write an algebraic expression for the function. Many mathematicians as well as Engineers, scientists, economists and others spend a great deal of effort building algebtaic expressions that approximate curves that arise from experimental data.
Penny
We received a followup question:
I found in a calculus book that I can use the Newton method to find the zeros of the inverse of this equation, but this method is really hard. I would like to know if there is a easier method to find the zeros of the inverse of this quintic equation.
Finding the zeros of the inverse function is much easier than what we have been attempting to do.
Graphically the zeros of a function are the x-coordintes of the points where the graph crosses the x-axis. In the graph of the inverse above the red dot shows where the graph crosses the x-axis. This point has coordinates (z,0) for some number z, and this number z is the zero of the inverse function. But the point coloured red in the graph of the inverse comes from the point coloured red in the graph of f(x). This point on the graph of f(x) has coordinates (0,z). Since this point is on the graph of
f(x) = x5 + 3 x3 + 1
we know that
z = f(0) = 1
Thus the only zero of the inverse function is 1.
Algebraically you are looking for the zeros of f-1(x), that is you want any number z so that
f-1(z) = 0
But f-1(x) is the inverse of f(x) so if
f-1(z) = 0
then
f(0) = z
But f(0) = 05 + 3 03 + 1 = 1, so z = 1.
Penny