![]()
Who is asking: Student
Level: Secondary
Question:
Hi can you help me with this question I don't understand it at all!
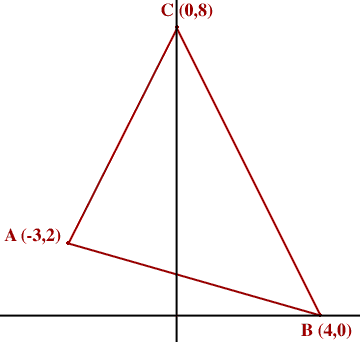
Find the Area of Triangle ABC
A(-3,2)
B(4,0)
C(0,8)
Thanks a lot!
Hi,
First draw a diagram,
I can see three methods to find the area of the triangle.
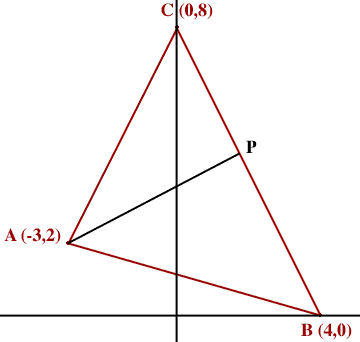
Method 1: The area of a triangle is half the base times the height.
Suppose that BC is the base. The height is then measured by constructing a line segment from BC to A which is perpendicular to BC. Suppose that this perpendicular meets BC at P.
The slope of BC is -8/4 = -2 and hence the slope of AP is 1/2.
Write the equation of the line through A with slope 1/2 and find where this line meets BC, that is find P. Use the distance formula to find the lengths of BC and AP and then use the fact that the area of a triangle is half the base times the height.
Method 2. Heron's formula.
Use the distance formula to find the lengths of the sides AB, BC and CA. Use Heron's formula to find the area of the triangle.
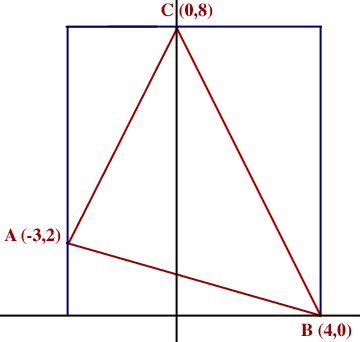
Method 3. Scissors and paste.
Inscribe the triangle ABC in a rectangle.
The rectangle has area 7
8 = 56 square units.
Cut out the rectangle and the cut along the lines AB, BC and CA. The rectangle falls into 4 pieces, one of which is the triangle ABC and the other three are right triangles. The base and height of these three right triangles are easy to find so the areas of these three triangles are easily calculated. The area of ABC is then
56 - the sum of the areas of the three right triangles.
Penny