Name: Crystal
Who is asking: Student
Level: Secondary

Question:
I am trying very hard to understand Absolute Value, and I cannot seem to grasp the idea. I do not know why we use it, what the point of it is. I do not know how to use it. I know that it is always positive or zero, and I assume it relates to distance, but how can you use it in equations. Please explain it to me as simply as possible, thank you.

Crystal

There are many ways to view absolute value. Graphically, it is simple. It is saying that five inches up the ruler is 'the same' as five inches down the ruler - both are +5. In a graph, you have taken the line y=x and broken it at x=0, reflecting the left hand side up into the positive numbers, so nothing goes negative and the graph has a mirror at x=0.

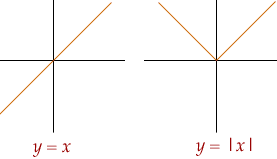
This breaking and looking at two sides - means that the algebra gets a bit wierd. There is no longer a simple formula, unless you know which side of x=0 you are on - OR you make up a new formula - |a|. [That is a trick mathematicians do, make up a new name for something that does not fit any previous name.]

The hardest is how to deal with it in solving equations. In eqations, the only ways I have confidence in are:

1. isolating the |a| and squaring, since |a²| = a²;
   
2. plugging in numbers to search for solutions and patterns;
   
3. cases - what is true for one interval or another on the line.

The second and third ideas are just putting the graphic experience into number and algebra. It is not great, but it is better than not being able to say what needs to be said - this is a number and it is positive whether you were going up or down when you calculated it!

The first is a trick because of the way squaring also gets rid of negative signs, and bends things up into a pattern symmetric about x=0. There is actually NO reason one should expect that something 'new' like this will fit well with previous experience with algebra. It does not fit with easy methods of 'solving for x'. It does fit well with issues of balancing equations, moving things around the = sign, etc. You will find, as you learn more, that lots of equations are hard to solve! And there are things mathematicians have learned to do when that happens.