hi my name is crystal and i am a high school student at bloomington high and i am in the 12 grade i would really appreciate it if you can answer the following question.
(question) step by step can you show me how to calculate the area of
the region inside the hexagon but outside the seven circles. given the
radius of each circle is one inch
(hint:you will have to use foil at some point)
Hi Crystal,
I am not at all sure I am solving the correct problem since you didn't supply a diagram. The diagram I see is below.
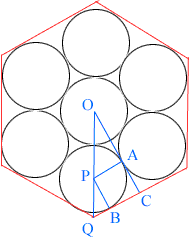
O and P are centers of circles, the line segment OC passes through A, the point where the two circles touch, and B is the point where the circle and the side of the hexagon are tangent.
By the symmetry angle QCO is a right angle. Since OC is tangent at A to the circle with center P and PA is a radius of the circle, angle CAP is a right angle. Similarly angle PBC is a right angle. Hence angle APB is also a right angle. Since |PA|=|PB|=1, APBC is a square. Thus |BC|=1.
Now consider triangle PQB. The measure of angle PQB is 60o and |PB|=1, hence |QB|=1/sqrt(3). Thus |QC|=1+1/sqrt(3) and hence the lenght of the side of the hexagon is 2+2/sqrt(3).
Now that you know the side length of the hexagon you can find its area. Subtract from this area 7 times the area of a circle with radius 1.
Penny