Name: David

Who is asking: Other
Level: All

Question:
I have a plot of land that I cannot find the square footage of. Actually my home sits on a large lot. Local building codes require that a home is seated on no less than 7500 square feet of land and have no less than 50ft of road frontage (the rear of the lot has 65ft of frontage on another road). I need to know if I have enough square footage to build a second home on the rear lot. The lot has five sides. Only one angle is a 90 deg. angle. The others I cannot determine. Of the 4 remaining angles, all 4 angles are obtuse, or greater than 90 deg. The dementions are 89.19' x 130' x 118.52' x 65' x 170.94'. The two legs that make the 90 deg angle are 89.19' and 170.94'. The measurements fall in order using the 90 deg angle as the point of origin and proceeding clockwise, 89.19', 130', 118.52', 65', 170.94'. I have used all the skill I can muster, however, it has been a long time since school and regretably I cannot find an answer. Anyones assistance is greatly apreciated.

I have sketched a rough diagram (not at all to scale) and labeled the vertices. The right angle is at B and I drew the line AC.

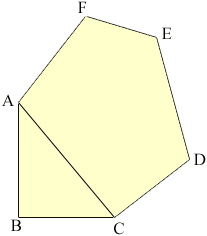
You can find the area of the triangle ABC but knowing the lengths of the remaining sides of the lot does not determine its area. Suppose that the sides CD, DE, EF, FA ans AC are sticks that are hinged at the vertices. The shape of the lot and its area can be changed by changing the angles without changing the lengths of the sides. You say that you don't know the angles. You can determine the area if you know the lengths of some diaginals. In particular if you know the lengths of AD and AE then you can use Heron's Formula to find the areas of the triangles ACD, ADE and AEF, and thus the area of the plot.