Please refer to figure in attached file. P is a point on the chord AB of a circle such that the tangent PT which touches the circle at T is equal to AB. How do we prove that PT² = AP x BP.

Name: Diego (Student)
Level: Secondary

The relationship that PT² = AP x BP is true for any point on the tangent line.

I have reconstructed your diagram below, added the point M at the center of the circle, and constructed the line segments MB, BT and TM.

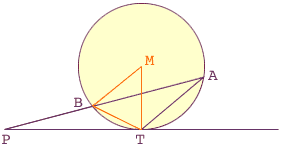
There are two facts about circles that you need to use.

1. Since PT is tangent to the circle at T and MT is a radius of the circle, the angle PTM is a right angle.
   
   
2. The chord BT is the base of two angles, TMB and TAB, the first with vertex at the center of the circle and the second with vertex on the periphery of the circle. Hence the angle TMB is twice the angle TAB

Now examine the triangles BPT and TPA. The angle BPT is common to both triangles and angle BTP = angle BAT, thus triangles BPT and TPA are similar. Hence

 ^PB/_PT = ^PT/_PA, or PAPB = PT²

Comment: In a problem involving a circle always introduce its center, and in a problem involving a tangent line to a circle always draw the radius which goes through its touching point and is perpendicular to it.