name: Geoff
question level: calculus AB (12th grade)

A recent lecture in my calculus class led me to realize that the derivative of the area of a circle, with respect to the radius is equal to the circumfrence. more logically:

d
--- (pi) r² = 2(pi) r
dr

this also holds true for the relationship between the volume of a sphere and the surface area of that sphere:
d
--- 4/3 (pi) r³ = 4(pi) r²
dr

why do these hold true? why is it only for circular objects?

Hi Geoff,

Think of the derivative as a rate of change. If a circular disk is growing then the derivative of the area function with respect to the radius measures how fast the area is changing relative to how fast the radius is changing. If the radius is r and it increases a small amount, say r^* then the area of the disk as increased by the area of band around the disk of thickness r^*.(The red band in the diagram below.)

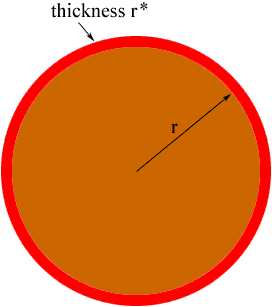
The area of this band is approximately the circumference of the disk times its thickness, that is

2 pi r r^*

The radius changed by an amount r^* thus the change in area relative to the change in the radius is approximately

 ^{2 pi r r*}/_r^* = 2 pi r

A similar argument holds for the volume of a sphere. If the radius increases a small amount then the volume changes by the volume of a shell around the sphere, like the layers of an onion. This shell has volume which is approximately the sufrace area of the sphere times the thickness of the shell.

The same argument does hold for the area of a square or volume of a cube but you need to be careful how you measure. Suppose that you have a square then let x be the distance from the center of the square to the midpoint of one of the sides.

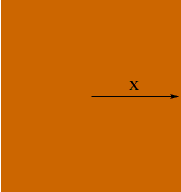
The area of the square is 4x² and its derivative is 8x, the perimeter of the square.

Try it with a cube.

Harley

Go to Math Central