I have a problem for a 10th grader?

Question 1.
What is the probability of choosing the longest diagonal in an octagon?

Question 2.
Probability of choosing the shortest?

Thanks,
Glenn

Hi Glenn,

I am going to assume that you are dealing with a regular octagon.

First you need to know how many diagonals a regular octagon has and then how many have the longest length. Draw an octagon, select one vertex and construct each diagonal from this vertex.You will see there are 5 such diagonals.

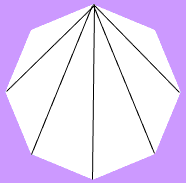
Thus for each of the 8 vertices you can draw 5 diagonals and hence you have constructed 5  8 = 40 diagonals. But you have constructed each diagonal twice, once from each of its ends. Thus there are 20 diagonals in a regular octagon.

A look at the diagram above shows that one of the diagonals constructed is longer than the others. Thus you construct one long diagonal from each vertex, and hence 8 long diagonals. Again you have constructed each one twice so there are 4 long diagonals. Thus if you select one diagonal from all the diagonals in a regular octagon there are 4 chances in 20 that you will select one of the longest ones, and hence a probability of  ⁴/₂₀ = ¹/₅.

What about the shortest?

Andrei and Penny

Go to Math Central