Question:
The label on a bottle of liquid detergent shows contents to be 12 ounces per bottle. The production operation fills the bottle uniformly according to the following probability density function:
f(x) = 8 for 11.975 ≤ x ≤12.10
and
f(x) = 0 elsewhere
a. What is the probability that a bottle will be filled with 12.02 or
more ounces?
b. What is the probability that a bottle will be filled between 12 and
12.05 ounces?
c. Quality control accepts production that is within .002 ounces of number
of ounces shown on the container label. What is the probability that
a bottle of this liquid detergent will fail to meet the quality control
standard?
In my mind I see a graph of the density function.
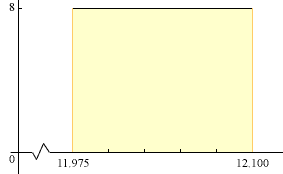
Notice that the scales an the X and Y axes are not the same and there is a break in the X-axis between 0 and 11.975. Notice also that the arera under the curve, that part shaded yellow, is 1 as it must be for a probability density function. I am going to do part b), and you can do parts a) and c).
In b) you want the probability that x is between 12 and 12.05. On the diagram that is the area under the density function, between 12 and 12.05, the region shaded red in the diagram below.
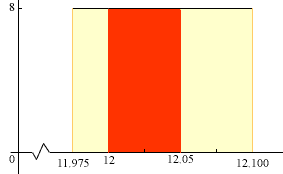
This region is a rectangle so it area is the length times the width, that is
(12.05 - 12)
8 = 0.05
8 = 0.4
Thus the probability that a bottle will be filled between 12 and 12.05 ounces is 0.4
Cheers,
Penny