Quandaries and Queries
Name: jaidev
Who is asking: Student
Question: Is there any general equation for a sphere?
Hi Jaidev,
I expect you know that the equation of the circle of radius r, centered at the origin, is
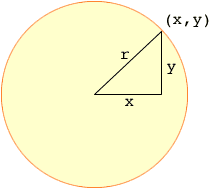
The point (x,y) is on the circle if and only if the right triangle with legs of length |x| and |y| has hypotenuse of length r, that is
For a sphere you need to use Pythagoras' theorem twice. In the diagram below O is the origin and P(x,y,z) is a point in 3-space. P is on the sphere with center O and radius r if and only if the distance from O to P is r.
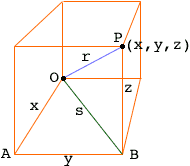
The triangle OAB is a right triangle and hence x2 + y2 = s2. The triangle OBP is also a right triangle and hence s2 + z2 = r2. Hence the distance |OP| from O to P satisfies
Similarly (x,y,z) is on the sphere with center (h,j,k) and radius r if and only if