Quandaries and Queries
  

 

My name is James. This is a secondary level question.  I am a student. 
 
This question is about finding bearings.  A boat race starts from
point A, goes North to Point B, a distance of 1000 meters.  The
course is triangular.  The bearing from point B to point C is South
70degrees West.  The distance from Point B to point C is 1500
meters.  Find the course bearing from C to A. 

I'm not sure which angle of the implied triangle to use for the
bearing and which directions to give(North,South,East, or West)

I constructed a triangle with points A,B, and C.  I tried to use the
Law of Sines to find Angle C.  I did 1500/sin70 = 1000/sin C to find
C to be equal to 38.7 degrees.  With this knowledge, angle B must
equal 71.2 degrees.  Using the Law of Sines again where side
b/sin71.2 = 1000/sin38.8, and I found side b to equal 1514.(Side b
being the distance from C to A).  Would the bearing from C to A
therefore be S 71.2 E? Thanks. 

 

 

Hi James,

I drew a diagram of the triangle you described and added a North-South line at C. I agree that the bearing from C to A is S 71.2o E. There is a good explanation of bearings at a page kept by David Levesen, a faculty member in the Department of Geology at Brooklyn College, City Uiversity of New York.

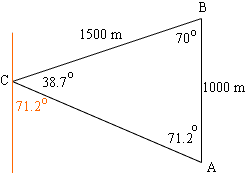
There is however a problem with your solution. In your use of the Law of Sines you have 1500/sin(70). But the side of length 1500 m is not opposite the angle at B.

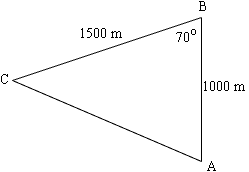
First you should use the Law of Cosines to find the length of CA.

|CA|2 = 10002 + 15002 - 2 1000 1500 cos(70o)

Once you know |CA| you can use the Law of Sines to find the angle at C.

|CA|/sin(70o) = 1000/sin(C)

Penny

 
 

Go to Math Central