![]()
Quandaries
and Queries
Can you help me understand why the area of a equilateral triangle is the square root of 3 divided by 4 times the lenght of the side squared?
student
Hi,
I drew a diagram of an equilateral triangle.
Draw a line from the vertex to the midpoint of the base.
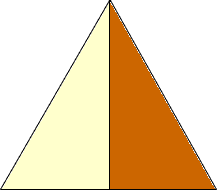
Cut along this line and move half of the triangle to form a rectangle.
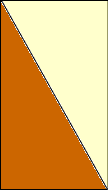
If a is the length of a side of the equilateral triangle and h the height then this rectangle has area
1/2
a
h
The triangle below, which is half of the rectangle, is a right triangle,
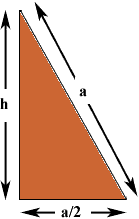
and hence, by Pythagoras' theorem
a2 = h2 + ( a/2)2
Thus h = sqrt( 3/4 a2) = sqrt(3)/2 a. Hence the area of the triangle is
1/2
a
h = sqrt(3)/4 a2
Penny