Quandaries and Queries
  


HELLO MY NAME IS JASON AND I AM TRYING TO SOLVE A TRIG PROBLEM AND HAVE FORGOT HOW TO DO IT. WHAT I HAVE IS A RIGHT TRIANGLE WITH SIDE A BEING 14 FEET AND SIDE B BEING 3 FEET, USING PYTHAGOREAMS THEOREM SIDE C SHOULD EQUAL 14.318 FEET ON A RIGHT TRIANGLE BUT I AM TRYING TO REMEMBER HOW TO FIND MY ANGLES OTHER THAN THE ONE THAT IS 90 DEGREES. CAN YOU PLEASE HELP ME? I NOT ONLY WOULD LIKE THE ANSWER BUT HOW TO DO IT AS WELL FOR FUTURE REFERENCE.

I HAVE BEEN OUT OF SCHOOL FOR 15 YEARS.



Hi Jason,

For a right triangle like you have, focus on one of the angles that is not 90 degrees. In the diagram below I have called that angle t.

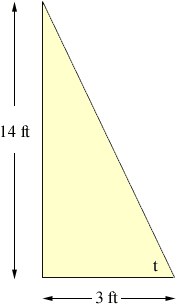
There are standard trig functions of this angle, in particular sin(t), cos(t) and tan(t). I want to focus on the tangent of t, tan(t). The tangent of t is defined as the ratio of the "opposite side" to the "adjacent side". So in your triangle tan(t) = opposite/adjacent = 14/3 = 4.667. To find the angles you need to use inverse trig functions. These are simetimes written sin-1, cos-1 and tan-1 or sometimes arcsin, arccos or arctan. On my calculator the inverse tangent is called atan. tan-1(4.667) is the angle whose tangent is 4.667. You need a calculator with the inverse tangent or inverse trig tables to find the value. I get tan-1(4.667) = 77.91 degrees.

One last warning. Some calculators measure angles in degrees but also in radians. If you use a calculator make sure it is set on degrees when you find the inverse tangent.

Penny


Go to Math Central