Jaye
Student
Secondary Level Questions
This is my first question:
Two force, 120lb and 200lb, act on a body and make a 52 degree angle w/ ea. other. What's the magnitude of the resultant of the forces and what is the measure, to the nearest degree, of the angle that it makes with the 200lb force?
This is my 1st answer(i don't know what im doing!):
R=(120 + 200COS52, 200SIN52)= (243.132, 157.602)LB = 289.744LB
I don't know if thats right, and I have no idea how to get the angle between.
Can you show me how to do the problem -- correctly?
.....................................................................
This is my second question:
I've tried a million different ways to do this problem, but I don't know the
correct way. This is it:
An airplane w/ air speed 350 mph is flying on a heading of 53 degrees. The wind is blowing from due north at 28 mph. What is the ground speed of the plane and its course?
Also, what is meant by course?
Thanx
Hi Jaye,
The "number" is correct for your solution to part one of the first problem, but I don't like what you have written.
The resultant vector is
(120 + 200COS52, 200SIN52)= (243.132, 157.602)
The magnitude of this vector is
Sqrt(243.1322 +157.6022) = 289.744
The diargam I see that goes with this solution is
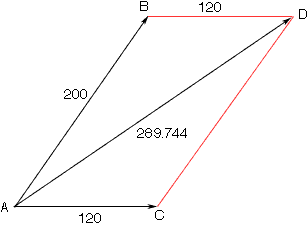
The angle measurement of BAC is 52 degrees and the vector AD is the resultant vactor. The angle you want is BAD and you know the lengths of the sides of the triangle BAD so you can find the angle you need using the Law of Coaines.
For problem two the course of the plane is the direction it is flying as a result of its airspeed, heading and the speed and direction of the wind. This time the diagram I see is
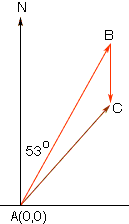
The vector AB is the air speed of the plane so the length of AB is 350. The vector BC represents the wind so its length is 28.
You can write the co-ordinates (x,y) of B in terms of the sine and cosine of 37o (37 = 90 - 53). C then has coordinates (x, y - 28). Once you have the co-ordinates of C you can find the length of AC which is the ground speed of the airplane. Finally use the Law of Cosines to find the angle BAC and hence the direction (course) of the airplane.
Penny