I have a question on the tangent to a quadratic curve.
Say I have a curve y = ax² + bx + c. The gradient, using the derivative of y, at any point x on the curve is: 2ax + b right? Then, for the tangent that cuts the curve at a point x, the equation of the tangent can be: y₁ = (2ax + b)x₁ + d.

My question is, how is the point d of this tangent determined? It is the point on the y-axis where the tangent cuts isn't it? Is there a formula for it?

Hi,

I drew a diagram of what you described with one change in notation. Since you are using x as the independent variable to describe an arbitrary point on the parabola I used p as the first coordinate of the specific point on the parabola where you have constructed the tangent. I called the second coordinate of this point q.

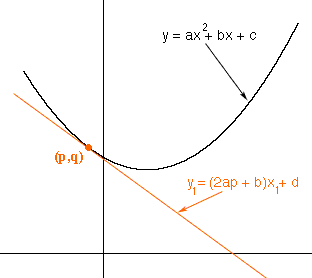
Since the point (p,q) is on the parabola you can find q,

q = ap² +bp + c

The point (p,q) is also on the tangent line so the coordinates p and q satisfy the equation of the line. Thus

q = (2ap + b)p + d

and hence

d = q - (2ap + b)p

Penny

Go to Math Central