Good morning,
I am a student trying to solve math problem. I'd like to calculate the radius of the circle that exactly fits any three points. If the points are (X1,Y1), (X2,Y2), and (X3,Y3), what is the radius of the circle that contains those three points?
Thank you very much,
Jim
Hi Jim,
The standard construction is illustrated in the diagram.
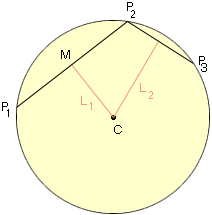
If P1, P2 and P3 are distinct points on the circle, L1 is the right bisector of the line segment from P1 to P2 and L2 is the right bisector of the line segment from P2 to P3 then L1 and L2 meet at the center C.
If each Pi has co-ordinates (xi, yi) and M is the midpoint of the line segment from P1 to P2 then M has co-ordinates ((x1+x2)/2, (y1+y2)/2). The slope of the line L1 is the negative reciprocal of the slope of the line through P1 and P2 and thus the equation of L1 is
y - (y1+y2)/2 = (x1-x2)/(y2-y1)
(x - (x1+x2)/2)
In a similar way find the equation of L2 and then solve this pair of equations to find the co-ordinates of C. The radius of the circle is then the distance from C to P1.
Penny