f(x)= 4/x
D:(-oo,0) U (0,oo)           R:(-oo,0) U (0,oo)  

f(x)= 0.5x^3 + 2  
D:(-oo,oo)        R:(-oo,oo)   

f(x)= x + sqrt(4-x^2)
D:[-2,2]     R:[-2,2sqrt(2)]

f(x)= sqrt(x+2)/(x+2)   D: (-2,oo)

f(x)= sqrt[(1/x) + 2]    D: (-oo,-.5) U (0,oo)

Hi JJ,

I agree with the first three. I also agree with the domains you have for the last two. Ther isn't a general way to determine the domain and range of functions so the firs thing I did with the last two is to graph them. I used the computer program Mathematica to graph the equations. If you have a graphic calculator you can graph them using it. This is one of the few places where I think a calculator is a useful device.

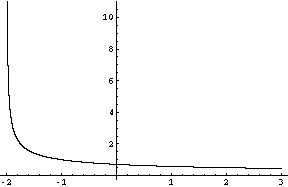
Graph of f(x)= sqrt(x+2)/(x+2)

Now I can see what is happening. When x is close to -2 (a little bit larger than -2) f(x) is close to plus infinity, and as x approaches plus infinity, the value of f(x) approaches zero. Also of x is in the domain then x is larger than -2 so the denominator is positive. The numerator is never negative so f(x) is never negative. Hence the range of f(x) is (0, +oo).

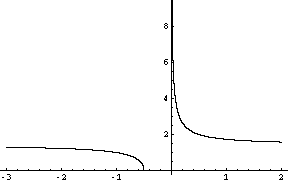
Graph of f(x)= sqrt[(1/x) + 2]

Since sqrt[*] is non-negative, f(x) > 0 for all x in the domain of f(x). Also as x approaches minus infinity, 1/x becomes very small so f(x) approaches sqrt(2). On the branch of the function with x > 0, as x approaches infinity, f(x) approaches sqrt(2). Hence the range is the union of (0,sqrt(2)) and (sqrt(2),oo).

Penny

Go to Math Central