Quandaries
and Queries
A dodecahedron has twelve faces, all of which are regular pentagons. Three edges meet at each vertex of the dodecahedron. An interior diagonal is a segment connecting two vertices such that the segment is not an edge or along a face of the dodecagedron. How many interior diagonals does a regular dodecahedron have?
Thank you
Joshua (10-12)
Hi Joshua,
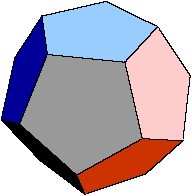
You should answer this in two steps. First you could count how many vertices there are, that will tell you how many pairs you could join in total; from this you then need to subtract the number of segments that correspond to edges and diagonals across faces.
Penny