Quandaries and Queries
  


Who is asking: Student
Level: Secondary

Question:
How far apart, assuming no obstacles, can two people stand and still see each other?

i know this deals with the curvature of earth, but i can't figure out the formulas involved.

thanks!



Hi Judy,

In the diagram below r is the radius of the earth, approximately 3963 miles, and h is the height, in feet, of a person standing in the surface of the earth, and C is the center of the earth.


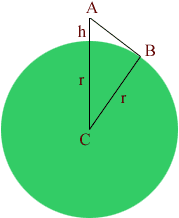
First notice that the height of the person in miles is h/5280. The line segment AB is the line of sight of this person to the horizon. Since AB is tangent to the circle, the angle CBA is a right angle. Thus, using Pythagoras' theorem, the length of AB is given by sqrt[(r + h/5280)2 - r2] But (r + h/5280)2 - r2 = (r + h/5280 - r)(r + h/5280 + r) = h/5280(2r + h/5280)  h/5280 is much smaller then 2r, hence 2r + h/5280 is approximately 2r and thus (r + h/5280)2 - r2 is approximately 2rh/5280 Substituting r = 3963 miles give the neat result that if your eyes are h feet above the earth, then the distance to the horizon IN MILES is about sqrt( 3*h/2) miles.

Thus a person 6 feet tall standing on level ground can see for about 3 miles. So, theoretically, a person 6' tall (with binoculars) should be able to see the top of the head of a six-footer who is 6 miles away. He would see the whole person at a distance of 3 miles.

Chris


Go to Math Central