![]()
Who is asking: Student
Level: Secondary
Question:
the inner rail of a race track is a perfect ellipse. the track is a
standard width all the way around. how can i prove that the outer
rail is a ellipse?
should i use the formula for foci?
thanks!
Hi Judy,
The general feeling here was that the outside rail does not form an ellipse so I looked at an example. Suppose that you have the ellipse
x2/4 + y2 = 1
and the track is one unit wide so that the outer rail goes through (3,0), 0,2), (-3,0) and (0,-2). The ellipse that passes through these points is
x2/9 + y2/4 = 1
I then took the point P ( 2/sqrt(5), 2/sqrt(5)) on the inside ellipse and calculated the distance to the point Q on the outside ellipse.
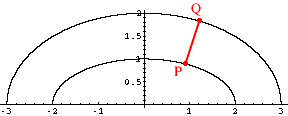
What is the point Q? I think that you should measure in a direction "perpendicular to the inside ellipse".To do this I used calculus to find the slope of the tangent to the inside ellipse at P (the slope is -1/4) and then wrote the equation of the line through P that is perpendicular to this tangent, ie the line through P with slope 4.This line intersects the outside ellipse at (1.13696, 1.8508). The distance from P to Q is 0.9866 and thus at this point the width of the track is less than 1 unit. Hence the outer rail is not an ellipse.
We are curious where this problem came from. Was it an assignment?
Penny