Quandaries and Queries
  

 

Name: Justina
Student
Secondary Level Questions
 
i cant figure out the range of this equation in interval form because the highest point seems to be a decimal. please help

f(x) = x + sqrt(4-x2)

The domain i think is [-2,2] and the range is [-2,?
 
 
.............................................................................
 
Building Design A circular air duct of diameter D is fit firmly into the right-angle corner where a basement wall meets the floor (see figure). Find the diameter of the largest water pipe that can be run in the right-angle corner behind the air duct.

I've been stumped by this question it seems like forever. I can only find the length of the square's diagonal, which leads me nowhere, since there is a tiny space where the air duct meets the floor. The figure is just a square. Inside is inscribed a large circle and in one corner is a small circle. Help!!
 

 

Hi Justina,

You are correct, the domain is [-2,2].

For the range, f(sqrt(2)) = 2*sqrt(2) and using calculus, this can be shown to be the maximal value.

We have two suggestions for your second problem.

One that uses coordinates.

If the circular air duct is in the bottom left corner of the basement you can use the usual coordinate axis. (Otherwise you just turn around).

The (section of) the air duct is a circle with center (D/2, D/2) and radius D/2. The (section of) the water pipe will be a circle with center (c,c) which will meet the floor at the point (c,0) and the wall at (0,c). It will also meet the air duct at a point (t,t).

  1. Figure out how to write (t,t) in terms of the diameter D of the air duct.
  2. Figure out how to write (t,t) in terms of the radius c of the water pipe.
  3. Once you have solved these two parts, the two expressions of t give you an equation linking c and D, so you can write c in terms of D.

And one that doesn't use coordinates.

Using the same notation as above I drew a diagram.

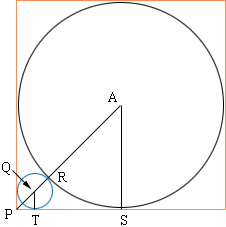
  1. The triangle APS is an isosceles, right triangle so Pythagoras' Theorem can be used to find |AP|.
  2. The triangle QPT is an isosceles, right triangle so Pythagoras' Theorem can be used to find |QP|.
  3. |AP| = |AR| + |RQ| + |QP|. Solve for c in terms of D.

Claude and Penny

 
 

Go to Math Central