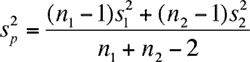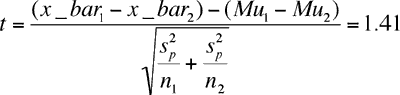Please help with this question.
Ms. Lisa Monnin is the budget director for the New Process Company. She would like to compare the daily travel expenses for the sales staff and the audit staff. She collected the following sample information.
At the .10 significance level, can she conclude that the mean daily expenses are greater for the sales staff than the audit staff? What is the p-value?
Sales ($) 131 135 146 165 136 142
Audit ($) 130 102 129 143 149 120 139
Having problems finding the p-value & unsure of the formula.
Kathy
Hi Kathy,
I am going to use Mu1 for the mean daily travel expenses for all the audit staff and M2 for the mean daily expenses for all the sales staff. The null and alternate hypotheses are
Null hypothesis: Mu1 = Mu2
Alternate hypothesis: Mu1 < Mu2
The corresponding sample means I will call X_bar1 and X_bar2. I got
X_bar1 = 130.29
X_bar2 = 142.50
For small, independent samples like you have the expression that you use for the variance depends on the assumptions you are making. I am going to assume that your teacher and textbook have you pool the data to estimate the variance using
From your data I got sp2 = 14.29 and the t-value is then
You were asked to test the hypothesis at a 10% level of significance so you can reject the null hypothesis and conclude that the alternate hypothesis is true if your computed t-value, 1.41, is larger that the 10% critical number for the t-distribution with 11 degrees of freedom. My statistics tables give the 10% critical number for the t-distribution with 11 degrees of freedom to be 1.363 so you can conclude, at the 10% level of significance that the daily travel expenses for the sales staff are larger than the daily travel expenses for the audit staff.
Finally the p-value which was really your question. I don't think of a formula for the p-value I think of a diagram. If the diagram below is the graph of the t-distribution with 11 degrees of freedom and the computed t-value, 1.41, is located on the horizontal axis then the area of the region shaded red is the p-value. If you want a formula it is Pr(t > 1.41).
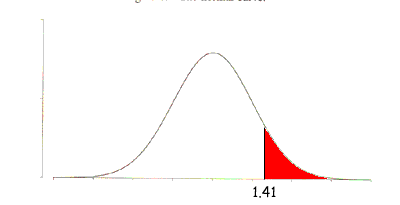
I can't give you a value for this area, the p-value, the best I can do is estimate it. From my table of the critical numbers of the t-distribution with 11 degrees of freedom I know that the 10% number is 1.363 and the 5% number is 1.796. Again I see diagrams of the t-distribution with 11 degrees of freedom. One for the 5% number
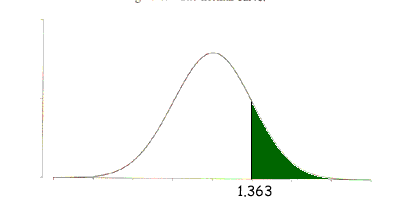
where the area of the region shaded green is 5%, and one for the 10% number
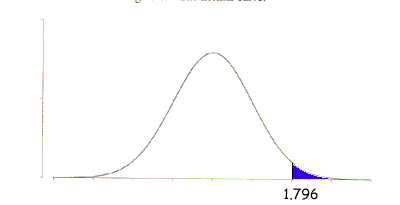
where the area of the region shaded blue is 10%.
By looking at the three diagrams I see that the area of the red region is smaller than the area of the green region, and larger than the area of the blue region. The area of the red region is the p-value of the test so I can say
0.05 < p-value < 0.10
Without better tables or a way to calculate the area under the t-distribution curve the best I can say is that the p-value is between 5% and 10%.
Harley