A vertically inverted cone( i.e. vertex down) has a radius 7
inches and height 24 inches. Water is filled to one third of its
height .Find the ht of water when cone is turned upside down
Hi,
When I read this problem I saw a conical shaped paper cup, one-third full of water. When you turn it over all the water runs out so the height s zero. But this is probably not the answer you want.
The important expression is that the volume of a cone is given by
volume = 1/3 pi
r2
where r is the radius of the base and h is the height. You also have to use some information about similar triangles. Below is a sketch of one cone inside another as you have in your problem.
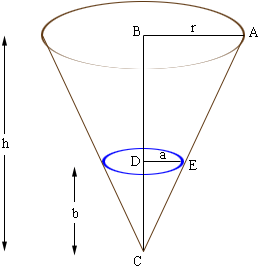
The triangle ABC and EDC are similar so
r/h = a/b
Using the volume expression, the volume of your cone is
cone volume = 1/3 pi
Use the similar triangle expression to find a and calculate the volume of the water in the cone by
water volume = 1/3 pi
The volume of air in the cone is (cone volume) - (water volume).
Now turn the diagram upsidedown. Again you have similar triangles.
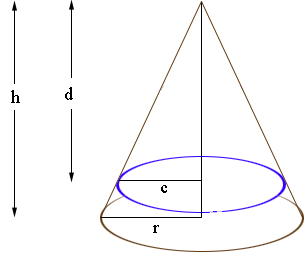
This time
h/r = d/c
Insert the values of h and r and solve for c in terms of d. Use the expression for the volume of a cone to write the volume of the air in terms of c and d. Use the volume for the air you found earlier and the expression for c in terms of d to form an equation in one variable d. Solve for d.
Penny