![]()
My homework question is:
Do all figures made up of two segments lie
in a plane?
(Hint: Consider two cases -- 1) the segments intersect,
or 2) the segments don't intersect. If the segments intersect, make
a triangle with one vertex at the intersection point and one side on
each of the two segments.)
MY question is about how to apporach this.
Are we talking
about two different planes here?
Laura
Hi Laura,
The important geometric fact here is that given any three points in three space that don't lie on a line, the three points lie on one, and only one plane.
For case 1 suppose that the two line segments intersect at a point A, as the two blue line segments in the diagram below.
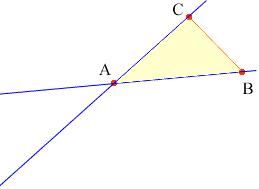
Take B and C to be points different than A, one on each line segment. There is exactly one plane that contains the points A, B and C. Since A and B lie on this plane, all the points on the line segment containing A and B also lie on this plane. Similarly all the points on the second line segment also lie on the plane. Hence, if the two line segments intersect then the answer to the question "Do all figures made up of two segments lie in a plane?" is yes.
For case 2 look at the box below and the red line segments. This box might be the room you are sitting in. One of the line segments is a line where the floor meets a wall and the other is where a wall meets the ceiling.
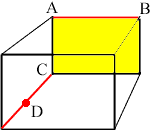
If the line segment containing A and B lie in a plane and the point C lies on this plane also, then the plane must contain the yellow wall of the box above. Thus the point D is not on the plane. Hence there is no plane that contains the red line segments.
Cheers,
Penny