![]()
Who is asking: Parent
Level: Secondary
Question:
Please help me with this law of Sines and Cosines problem.I'm trying
to help my daughter, but were both confused.
the question: On the one side of a stream lines PA= 586.3 feet, PB = 751.6 feet are measures, angle APB being 167 degrees and 36 min. Q is a point on the opposite side of the stream. Angle PAQ=63 degress and 18 min and PBQ=49 degrees and 24 min. Find PQ.
Hi,
Below is my diagram. I am not going to do the calculations but I can show you an approach to solving this problem. On the diagram I put a dot on a line segemnt if I know its length and a dot in an angle if I know its measure.(I extended AP to meet BQ at S.)
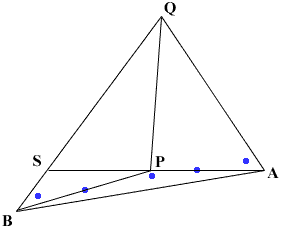
Since the measure of angle APS is 180 degrees I know the measure of angle BPS and hence the measures of angles PSB and PSQ. I can then use the law of sines on triangle SBP to find the length of PS. Thus updating my diagram with dots where I know values, I get
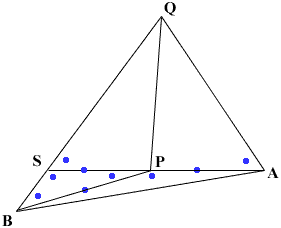
If I can find sin(AQP) then I can use the law of sines on triangle AQP to find the length of QP. At the moment I don't know this angle but, since the sum of the measures of the angles in a triangle is 180 degrees, I know the measure of angle AQS.
Using the law of sines on triangles AQP and PQS I get
|QP|/sin(PAQ) = |PA|/sin(AQP)
and
|QP|/sin(QSP) = |SP|/sin(PQS)
Solving these equations for |QP| and then setting them equal gives
|PA|sin(PAQ)/sin(AQP) = |SP|sin(QSP)/sin(PQS)
Write sin(PQS) = sin(AQS - AQP) and expand this in terms of sines and cosines of angles AQS and AQP. Substitute this expression into the above equation which then can be solved for sin(AQP).
I hope this helps,
Penny