My name is Nicolasa, a current student and the level of this question is secondary (10-12).
When is the limit of f(x) undefined?
Hi Nicolasa,
There is a technical definition of a limit of a function which is usually worded using the Greek letters delta and epsilon. The answer to your question is that the limit is undefined if the limit does not exist as described by this technical definition. I think, however, that this is not the answer you are looking for. What I will do is give you three examples of situations where the limit doesn't exist.
Example 1.
f(x) = 1/x2
This function exists for all nonzero values of x.
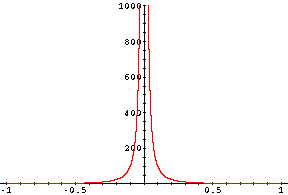
f(x) = 1/x2
In this example the limit of f(x), as x approaches zero, does not exist since, as x approaches zero, the values of the function get large without bound. The values of the function "approach infinity", by which I mean that they get large and do not approach a real number.
Example 2.
f(t) = 0 if t < 0
f(t) = 1 if t = 0
f(t) = 1 if t > 0
This is the function that represents the current flowing through the wire that connects the lamp on your desk to the wall socket. Here the variable t is time. The lamp is initially turned off and at time zero you turn on the lamp so the current jumps from zero to one unit at that instant, and remains at that value until you turn off the lamp.
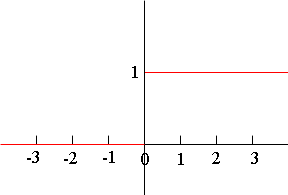
Here again the limit of f(t), as t approaches zero does not exist. The reason this time is that if t approaches zero from the left side it seems that the limit should be zero but if t approaches zero from the right, it seems that the limit should be 1. When such a situation arises the limit does not exist.
Example 3.
f(x) = 0 if x < 0
f(x) = 0 if x = 0
f(x) = sin( 1/x) if x > 0
For x larger than zero this function has a "wild" behaviour. It oscillates between -1 and 1 and the oscillations occour more rapidly the closer you get to zero. I only tried to sketch the graph for x between 0.01 and 0.15.
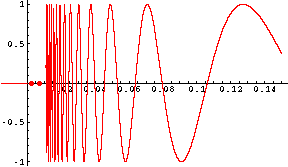
In this case as x approaches zero from the right the values of the function seem to get close to every number between -1 and 1 on the y-axis. Again, in this situation, the limit does not exist.
I hope this helps,
Penny