I am a student (10-12) secondary.

Please could you tell me why for my coursework (where I have to find the largest area that a fence 1000m long can cover) why I should only test equilateral and isoceles triangles? We were told NOT to do right angled triangles but I was wondering why not?

Thankyou very much
Petey

Hi Petey

Suppose that triangle ABC has a right angle at C and that the perimeter is 1000 m. Let M be the midpoint of BC. Construct an isosceles triangle PBC on the same base, BC, and with |CA| = |PM|. The triangles ABC and PBC have the same base and height and hence the same area. I want to show you that the perimeter of triangle PBC is less than the perimeter of triangle ABC.

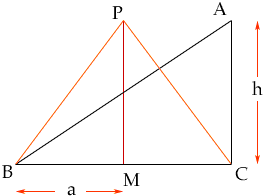
Claim: |PB| + |CP| = 2 |PB| < |AB| + |CA|.

Since all the lengths are positive it is sufficient to show that

4 |PB|² < (|AB| + |CA|)²

Let h = |AC| = |PM| and a = |BM| = |MC|. Using Pythagoras' Theorem,

|PB|² = a² + h²
and
|AB|² = 4 a² + h²

Thus

(|AB| + |CA|)² = |AB|² + |CA|² + 2 |AB||CA|
= 4 a² + h² + h² + 2 h Sqrt( 4 a² + h²)
> 4 a² + 2 h² + 2 h Sqrt(h²)
= 4 a² + 4 h²
= 4 |PB|²

Thus the perimeter of triangle PBC is less than the perimeter of triangle ABC. Hence if you move P upwards to the place where the triangles have the same perimeter you have a new isoscelese triangle PBC with the same primeter as ABC but a larger area.

Cheers,
Penny

Go to Math Central