The golden ratio

		Quandaries and Queries
	Name: Phillip Question: I am interested in Sacred Geometry and would be grateful if you could show me a geometrical proof for the following. The Golden Section can be made from an equilatereral triangle inscribed within a circle. The Golden Section is achieved by joining the mid points of two arms of the triangle to the circumference. I can prove this by erecting a perpendicular to the line outside the circle, but am interested to see how it can be proved from within the circle. Thank you. Hi Phillip, An easy proof depends on knowing that the golden section is the positive number that satisfies the equation x² = x+1. One also must know () If two chords of a circle intersect in a point that divides the first chord into the lengths a and b, and the second into the lengths c and d, then ab = cd. To apply this to an equilateral triangle ABC inscribed in a circle, let the sides of the triangle have length 2x. Thus the line segment that joins the midpoints M of AB and N of of AC has length MN = x. 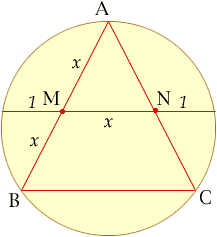If you extend MN in both directions to meet the circle, by symmetry one sees that the distance from M to the circle equals the distance from N to the circle. We choose that distance to be our unit length. We now have two chords through M; one is divided by M into lengths 1 and x+1 while the other has AM = MB = x. Using theorem () we get x*x = x+1, so x:1 must be the golden ratio. Chris
	Go to Math Central