![]()
Who is asking: Student
Level: Elementary
Question:
why cant an equal sided rhombus have 3 lines of symmetry? you have
one line of symmetry on each of the diagonals, and there should be
one vertically
on an angle. can you please explain the rules of symmetry to me? thank
you!
Tonia
There are two parts to this answer.
You are right about the two diagonals being lines of symmetry. Moreover, these two lines meet at 90 degrees, so together they make a half-turn.
If you start with just that symmetry - something you would get by folding a piece of paper to make one line, then folding that edge back onto itself, making the second perpendicular line, a single cut near the shared corner will cut four layers of paper and cut off a rhombus.
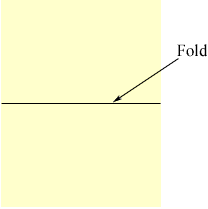
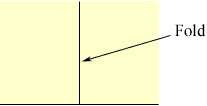
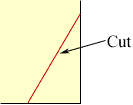
So those two symmetries are enough, and a general cut or general rhombus will not have any more mirrors.
HOWEVER, there are SOME special cases where you do have a third (and fourth) line. This will make a square - which is a special type of rhombus. Not only are all the sides equal, but all the angles are equal as well. For these special cases, the third line meets the first two, of the diagonals, at 45 degrees, and is a mirror splitting opposite sides.
So there are two different questions you might
be answering:
- Is there a rhombus with only two lines of symmtry? The answer is
yes, if you take something like a long thing 'diamond' shape, from
a cut in the folding above.
- Is there a different rhombus which does have more that two lines of symmtery? The answer is yes as well - the square does that.
You can play with examples (a program like Geometer's Sketchpad is great for such play) and see that IF there are three lines for any figure with only four vertices, a,b,c,d, then there will be four lines and the figure will be a square.
This is possible to observe, but not easy to prove except by looking carefully at the possible places vertex a can go under such a symmetry. You will find that if a can go to two other vertices, then it can go to all three other vertices. This will show the four angles are the same as well - so you do have a square.
Walter Whiteley