Quandaries and Queries
  


I am working on a craft project at home and I have been given the following information:
16" tall and 13" diameter at base, with 1 and 1/2 " opening at top.

Is there a basic formula for creating a cone with this info?

My name is Tracie.
Thank you.



Hi Tracie,

The cone can be made by rolling a trapeze whose bottom side is roughly 4.71 inches and top side roughly 40.84 inches, and whose height is 17 inches.

(The bottom and top side are obtained by multiplying the diameters 1.5 and 13 by , and the height is obtained by applying the pythagorean formula to find the hypothenuse of a right triangle whose dimensions are 16 and (13 - 1.5)/2.)

In the diagram below of the cone, triangles ADB and APC are similar and hence,

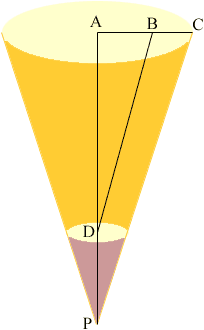
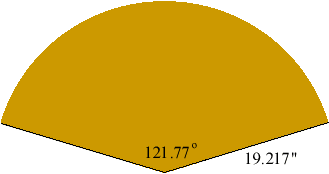
 |AB|/|BD| = |AC|/|CP| Hence |CP| = 13/2 17/(11.5/2) = 6.5 17/5.75 = 19.217"
The length, a, of an arc of a circle of radius r is given by a = r theta where theta is the angle at the center of the circle, measured in radians. In the diagram below the arc has length a = 40.84" and the radius is 19.217" and hence theta = 2.125 radians which is 121.77o.

Hence to create the cone draw a circle of radius 19.2", cut off a sector with angle 121.8o and then cut from the apex of this sector another sector of radius (19.2 - 17.0)".

Claude and Penny


Go to Math Central