Dear Math Central,
My name is Uneeza Aman, and I will be a senior in high school this year. I am having some trouble with my summer homework. This is supposed to be a review so I guess the problem is of secondary difficulty.
I checked the archive for some help, and I found this problem, which is similar to mine:
abs(x2 - 12x) = 8
However, my problem is an inquality:
abs(x2 - 4x) > 3
(a) I tried the problem myself and here was my first problem:
abs (x2 - 4x) = x2 - 4x if x2 - 4x > (or equal to) 0
abs (x2 - 4x) = 4x - x2 if x2 - 4x < 0
i get two answers for what x should equal and i dont know which one to use.
(b) But I dont think i really need that part to solve the problem, so I went ahead and set up the two parts:
if x2 - 4x> (or equal to) 0 x2 - 4x >3 then x > -.645, x> 4.645
------------------or---------------------
if x2 - 4x < 0 4x- x2 > 3 then x < 3, x < 1
This is where my real problem arises. I have two values which x should be greater and two values which x should be less. I dont think I can just pick one and I dont think it is an intersection. For example, if it was an intersection,
x > -.645 and x> 4.645
x < 3 and x < 1
then the answer would be x < 1 or x > 4.645
But that cant be the answer because x cannot equal 0 , 1, or 4. All are satisfied except the x cannot equal 0. Also, if that was the answer, x = 2 isnt included in that answer, and when x = 2, abs (x2 - 4x) > 3 is a true statement.
That is why I cant figure out this problem. I am afraid I messed up in part (a), but I still dont know. I can't figure out a complete solution without the trusty guess-and-check method.
Your help would be greatly appreciated. Thank you
-Uneeza
Hi Uneeza,
In these problems involving absolute values, you will need to use the algebraic recipes you used to solve other alegbra problems, but before that you need to use logic to get rid of absolute values: There is no "general rule" just common sense".
Now when x2 -4x > 0, you have abs (x2 -4x) = x2 - 4x and you want to find the values of x for which x2 - 4x > 3.
And when x2 -4x < 0, you have abs (x2 -4x) = -(x2 - 4x) and you want to find the values of x for which -(x2 - 4x) > 3, that is, x2 - 4x < -3.
So, your complete set of solutions will be the set of values of x for which x2 - 4x is either larger than 3 or smaller than -3.
You can avoid playing with inequalities if you know that the graph of x2 - 4x is "concave up": For very negative values of x, x2 - 4x is a large positive number, and when x starts moving towards the right side, the value x2 - 4x becomes smaller. At some point it will (or may) pass through the value 3, become yet smaller, then it will (or may) pass through the value -3, become still smaller, then start increasing again and pass again through the values -3 and 3, and become a large positive number again.
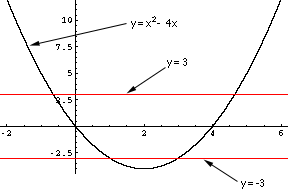
If you know that much, all you need to find out are the threshold points:
When is x2 - 4x equal to 3? and when is it equal to -3?
Claude