Name: wan
Who is asking: Student
Level: All
I am trying to find the radius
of an arc. The only things i know about the arc is all referenced from
the line of tangency to the arc. on both sides i have a differnt horizontal
perpendicular distance to the point of tangency.
left side |-------*---------------| right side (*=point of tangency). Then
i have 2 difference vertical perpendicular distance of the end points to
the line of tangency. I know it sounds very bad in text but this is all
i know about the arc. Can you help me find the radius?
Hi Wan,
I drew a diagram in the co-ordinate plane with the point of tangency at the origin O and the tangent line the X-axis. If a and b are the horizantal and vertical distances from the point of tangency to one of the endpoints of the arc then this endpoint is at (a,b). I called this point Q.
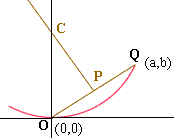
Let P be the midpoint of the line segment OQ and construct a perpendicular to OQ at P meeting the Y-axis at C.
Since OQ is a chord of the circle the center lies on the line PC. Since the X-axis is a tangent to the circle, the center is on the Y-axis. Thus the center of the circle is C.
Write the equation of the line PC. It passes through P which has co-ordinates a/2 and b/2 and has slope -a/b. The center of the circle is the point C(0,r) where this line intersects the Y-axis. The radius of the circle is r.
Penny