name: Weisu

secondary school
student

I have some questions about pre-calculus.
(1) (2(cos(x))^2)+3sin(x)-1=0
(2) sin(x)cos(x)=(1/2)
(3) 3sin(x)=1+cos(2x)
(4) tan(x)*csc(x)=csc(x)+1
(5) sin(arccsc(8/5))
(6) tan(arcsin(24/25))
(7) arccos(cos(11pi/6))
the last problem uses radian measure.

I tried the problems, and here is what I have so far:

(1) (cos(x))^2=1-(sin(x))^2, so substituting,
2(1-sin(x)^2)+3sin(x)-1=0. Distributing,
2-(2sin(x)^2)+3sin(x)-1=0. From here, I do not know
where to go.

(2) I don't know where to start here.
(3) I don't know where to start here.

(4) starting with the original equation, tan(x)*csc(x)
=csc(x)+1, divide both sides by csc(x):
tan(x)=1-sin(x). From here, I don't know what to do.

(5) I don't know where to start here.
(6) I don't know where to start here.
(7) I don't know where to start here.

Weisu

Hi Weisu,

I can help with a few of your problems.

1. You have so far 2-(2sin(x)²)+3sin(x)-1=0, that is -2sin(x)²+3sin(x)+1=0. This is a quadratic in sin(x). If you write y=sin(x) then this becomes -2y²+3y+1=0. This doesn't factor (are you sure that you have the original problem written down correctly) but you can solve it with the general quadratic
2. If you multiply both sides by 2 you get 2sin(x)cos(x)=1. But 2sin(x)cos(x)=sin(2x) so the problem becomes sin(2x)=1.
3. Expand cos(2x) in terms of sin(x) and this problem will aslo be a quadratic in sin(x) like problem 1.

For problems 5, 6 and 7 draw a right triangle and write down what you know. For example for problem 6.

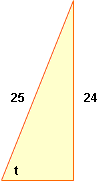
In the diagram sin(t) = 24/25, so tan(arcsin(24/25)) is the tangent of t. Use Pythagoras' Theorem to find the length of the third side of the triangle, and then find tan(t).

Penny

Go to Math Central