Given:Trapezoid ROSE with diagonals RS and EO intersecting at point M
Prove:Diagonals RS and EO do not bisect each other.
Now, my book gives me all the steps; however, one step, I don't understand. I hope you can help. I'll give you the step:
They first proved triangle I congruent to triangle II with SAS using an indirect proof. I understand that. But then they say OR is parallel to SE and the reason is," if 2 lines are cut by a transversal and alternate interior angles are congruent, then the lines are parallel."And then they go on to say that a trapezoid only has one pair of parallel sides and we just saw there are 2 pairs of parallel sides if diagonals RS and EO bisect each other so it can't bisect each other.
My question is: how do you know what the alternate interior angles are going on? You could say that OS is parallel to RE from that because if 2 lines, OS and RE, are cut by a transversal,RS, and alternate interior angles are congruent, then the lines, SO and RE are parallel. How do you know its the lines SE and OR being cut with transversal RS; thus, it being parallel and contradicting the given that the figure is a trapezoid?
Hi Abraham,
Below I have reproduced the diagram you sent.
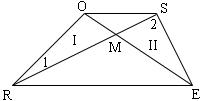
Your book gives a proof by contradiction. The authors first assumes that the diagonals do bisect each other. That is they assume that
|OM| = |ME| and |RM| = |MS|.
They then argue, using SAS that the triangles I and II are congruent, these are the triangles ORM and ESM. At this point you need to be somewhat careful as the diagram may be misleading. The assumption is that |OM| = |ME| even though they don't look the same in the diagram. Also |RM| = |MS| and hence the congruence of the triangles ORM and ESM implies angles ORM and ESM are congruent. Hence RS is a line that cuts OR and ES and the alternate interior angles (ORM and ESR) are congruent. Hence OR is parallel to ES.
I don't like this problem. I prefer the definition that "a trapezoid is a quadrilateral with a pair of parallel sides" rather than "a trapezoid is a quadrilateral with exactly one pair of parallel sides". With my definition a parallelogram is a trapezoid and the problem you were given could then be reworded as
Given:Trapezoid ROSE with diagonals RS and EO intersecting at point M
Prove:ROSE is a parallelogram.
Harley