The question is,"Triangle ABC is not isosceles.Prove that if altitude BD were drawn, it would not bisect AC."My question is If an altitude is drawn wouldn\'t that mean automatically its isosceles because, In a triangle the sides opposite congruent angles(in this case the right angles)are congruent?WHat am I thinking wrong? please go to for the diagram
http://www.nysedregents.org/testing/mathre/matharch/mathbtestau02.pdf
then #30 for the diagram.And I'm talking about the altitude, that it will create right angles on both sides. In a triangle the sides opposite congruent angles(in this case the right angles)are congruent so that would mean that the triangle is isosceles.Wouldn't it?You can always draw an altitude, thus making right angles thus proving its isosceles.
Hi Abraham,
The diagram given looks like
If you construct the altitude you get
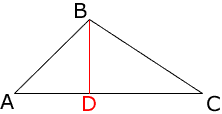
Certainly the sides AB and CB don't look congruent, and they are not.
I think the way to prove this is to say "Suppose that the altitude does bisect AC." Then AD and DC are congruent so triangles BAD and BDC are congruent by the side-angle-side theorem. Hence BA and BC are congruent and hence ACB is isosceles.
Hence, if the altitude bisects AC, then the triangle must have been isosceles to start with.
Harley