Hello,
I have the following equation:
y = ln(x) + x
How do I solve for x?
Thanks in advance
Alain
Teacher
Question for secondary
Hi Alain,
This is a nice question. The simple "flippant" answer is, you don't, but there is a lot more you can say.
I want to name this function using functional notation so I am going to use
y = f(x) = ln(x) + x
The challenge is to solve for x, that is to express x as a function of y. We usually think of x as the independent (input) variable of a function and y as the dependent (output) variable so I am going to change the instructions by saying
in the expression y = log(x) + x change x to y and y to x and then solve for y.
So I have x = log(y) + y and the instructions are to solve for y. If I could do it this would give an expression in x which I am going to call g(x). I can't do it algebraically but I can do it geometrically.
First plot the function y = log(x) + x. The domain of the function is all positive real numbers so I plotted it for 0 < x ≤5.
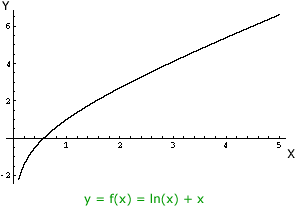
Next change x to y and y to x.
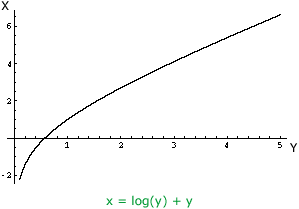
Notice that the variable names get changed in the function expression but also the X-axis becomes the Y-axis and the Y-axis becomes the X-axis.
The final algebraic instruction "solve for y" means, geometrically, "put the graph in standard position with the X-axis horizontal with positive to the right, and the Y-axis vertical with positive upwards". Rotating the graph and flipping it I get
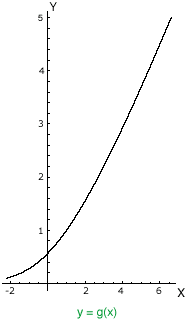
The point I am trying to make here is that y = g(x) is a perfectly good function, we just can't write it algebraically in a convenient firm. To be more precise g(x) can not be written in terms of polynomials, roots, logarithms, exponential functions or trigonometric functions.
I hope this helps,
Penny