alexandra
student grade 11
In triangle ABC, b=40, and angle A= 30 degres. What values of BC will give two solution for angle B?
Hi Alexandra,
I drew the situation you described but without the point B.
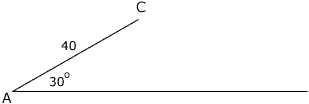
You are looking for configurations where you have two different points B1 and B2 on the ray through A so that CB1 and CB2 have the same length.
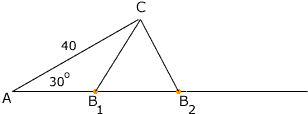
One way to find a pair of points B1 and B2 is to draw an arc of a circle, with center C, and a radius so that the arc cuts the ray through A at two points, B1 and B2. The radius of the circle is the length CB1 that you want.
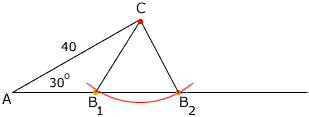
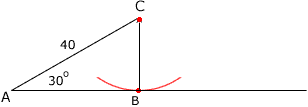
The question then is, what can the radius of the circle be if an arc cuts te ray through A at two different points?
If the radius is too large (larger than 40 units) then the circle will only cut the ray at one point. Thus CB1 can't be larger than 40. If the radius is too small the circle will not cut the ray at all. There is one value of the radius which results in the circle touching the ray at only one point. What is this radius?
Penny