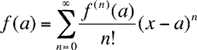Question:
i have to represent ln(x) as a power series about 2
i`m not getting the final answer which is ln 2+ sigma (((-1)(n+1)/
(n*2n))*(x-2)n). i don`t get the ln 2 part
i show you my trial
f(x)= ln x.
f-(x)=(1/x) .
f--(x)= (-1/x2)*1/2!
f---(x)= (2/x3)*1/3!
f----(x)= (-6/x4)* 1/4!
so the pattern shows me that f(n)= ((-1)(n+1))/xn *n)
so f(2)= sigma ((-1)(n+1))/2n *n) *(x-2)n
so as you see i don`t get ln 2
Anood,
The Taylor series expression for f(x) at x = a is
where f(n)(a) is the n-th derivative of f(x) at x=a if n ≥ 1 and f(0)(a) is f(a).
The series you developed for ln(x) at a=2 is correct for n ≥ 1 but what about the first term, that is n = 0?
The first term (n = 0) is f(0)(2)/0! (x-2)0
But 0! = 1 and (x-2)0 = 1 and hence the the first term is
f(0)(2) = f(2) = ln(2)
Penny