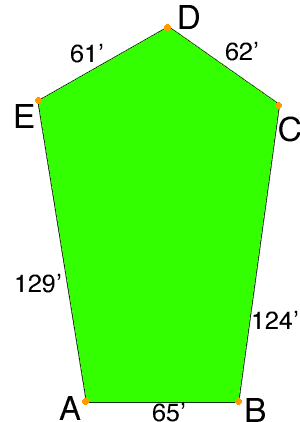
Is it possible to determine the square footage and acreage of a residential lot that's straight on 3 sides, and triangular on the 4th side?
As shown in the crude sketch below, the two legs of the triangle at the back end of the lot are 61' and 62'.
Sincere Thanks for the help.
Bob
61' __ 62'
__ ---- ---- __
__ ---- ---- __
| |
| |
| |
| |
129' | | 124'
| |
| |
| |
| |
|________________|
65'
Hi Bob,
The one word answer is no. The lengths of the sides don't give me enough information, I would need to know something else like the angles. I think I can convince you that I need more information.
Suppose that you drive a stake into the ground at each of the 5 corners of your lot. In the diagram I labeled the stakes A, B, C, D and E so that I can refer to them. I tried to draw it roughly to scale.
Now tie a 65 foot string between A and B, a 124 foot string between B and C, and continue around the lot until you are back to A.
Leaving stakes A, B and E in place, pull the stakes C and D out of the ground, leaving the strings attached to them. Move stake C over close to the string joining E and A and, keeping the string between B and C taught, drive stake C into the ground.
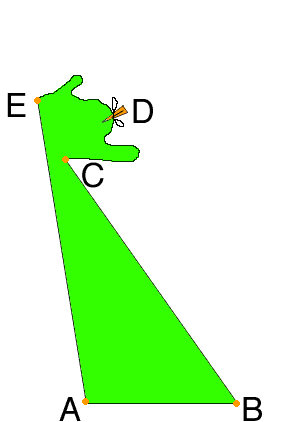
Finally take stake D and, keeping the string between D and C taught and the string between D and E taught, drive stake D into the ground. This gives you a strange shaped lot but with sides the same lengths as the original lot.
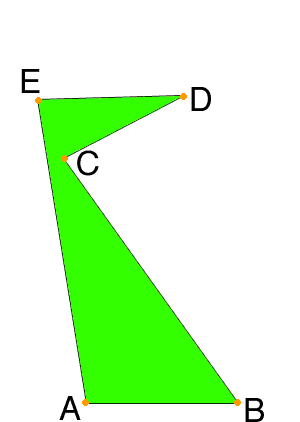
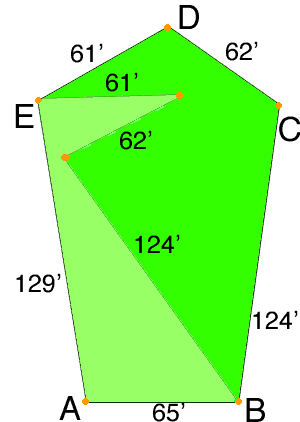
If you compare the two lots it is clear that the area of the original lot is much larger than the area of the new lot.
Penny