Hello, my name is Brad and I am a student with a Stat's math question. Please advise on solving for this problem below using the normal distribution method.
Thanks
The life of a toy is normally distributed. Suppose 92.51% of the items lives exceeding 2,160 hours and 3.92% have lives exceeding 17,040 hours. Find the mean and the standard deviation.
Hi Brad,
I drew a diagram of the normal distribution with mean mu and standard deviation sigma, and marked 17,040 hours on the axis. Since the probability of an item having a lifetime exceeding 17,040 hours is 3.92% or 0.0392, the probability that an item has a lifetime between mu and 17,040 hours is 0.5 - 0.0392 = 0.4608.
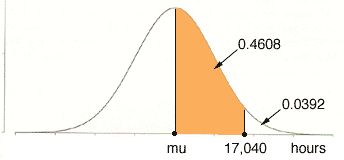
If you then convert this to the standard normal distribution using the conversion
z = (x - mu)/sigma
you get
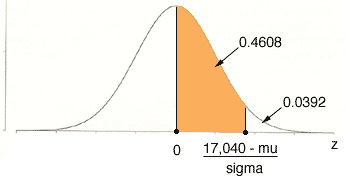
My normal table tells me that the probability that a standard normal random variable is between 0 and 1.76 is 0.4608. Thus
(17,040 - mu)/sigma = 1.76
This gives you an equation relating mu and sigma.
Now go through the same procedure using the fact that the probability of an item having a lifetime exceeding 2,160 hours is 92.51% to find a second equation relating mu and sigma. You can then solve these equation to find mu and sigma.
Be careful about signs when you find this second equation. The shaded portion of the diagram will be to the left of the origin so the z-value will be negative.
Penny