A cube has a volume of 64 cubic inches. What is the length of segment AB? Segment AB is a straight line from the top left corner of the cube to the lower right bottom corner. I know that each side of the cube is 4 from the formula for cubic volume x cubed = cubic volume and I tried using the pythagorean theorem for the segment AB and came up with 5.66 approx. which is incorrect the correct answer is 6.93 approx. or 4 times the square root of 3.

I am a parent of 9th grader and very curios myself how this answer is derived. Thank You for your helpful website but was unable to solve can you please explain how this problem is solved. Thank you so much. 

Brett

Hi Brett,

Pythagoras Theorem is exactly the tool you need, but you need to use it twice. I drew a sketch of a cube with sides of length 4 and labeled some vertices so that A and B are in the position that you describe.

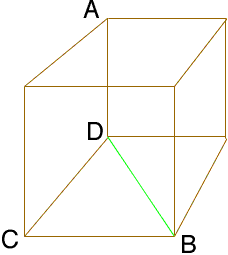
The line from D to B in the diagram completes the triangle DCB, which has a right angle at C. Thus, by Pythagoras' Theorem

|DB|² = |DC|² + |CB|² = 4² + 4² = 2 4²

and thus

|DB| = 4 √2

Now consider the triangle ADB

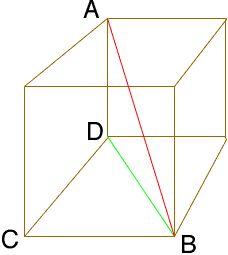
Triangle ABD is also a right triangle, this time with the right angle at D. Hence, using Pythagoras' Theorem again

|AB|² = |AD|² + |DB|² = 4² + 2 4² = 3 4²

and thus

|AB| = 4 √3

So the length is exactly 4 √3 units, which is approx. 6.93 units.

Penny

Go to Math Central