Question:
A lighthouse is located on a small island, 3 km away from the nearest point P on a straight shoreline, and its light makes four revolutions per minute. How fast is the beam of light moving along the shoreline when it is 1 km from P?
Hi,
Below is my diagram at an instance when the light is directed toward the shore.
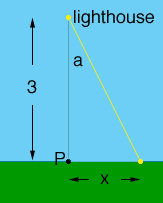
I let x be the number of kilometers between P and the point when the light hits the shore, and I let a be the measure of the angle between the line from the lighthouse to P, and the light ray. Both x and a change with time so x is a function of time t, x = x(t) and a also is a function of t, a = a(t). You are given information on the rate at which a changes, da/dt = a'(t), and you want to find the rate at which x changes when x = 1 km.
The relationship between a and x is that
x/3 = tan(a) or x = 3 tan(a)
If you differentiate both sides of this equation with respect to t you will get an equation that relates x'(t), a'(t).
Before you do this however you need to make sure that a(t) is expressed in radians and a'(t) in radians per minute. The light makes 4 revolutions per minute and each revolution is 2
radians, hence the light rotates at 8 radians per minute. That is
a'(t) = 8
Now differentiate the equation above to find the relationship between x'(t) and a'(t) and evaluate at the time when x(t) = 1.
Penny