Quandaries
and Queries
A company that sells x units of a product generates an income (I, in dollars) which is a function of x. The income generated is described by the equation
I = (-1/2)x2 + 100x.
Discuss how to determine the number of units that must be sold so that
the company can maximize its income. What is the maximum income?
CONNIE
PARENT
SECONDARY
Hi Connie,
I am not sure what is expected but I would sketch a graph of the function
I = (-1/2)x2 + 100x.
You can solve
(-1/2)x2 + 100x = 0
to see where the graph crosses the x-axis, and then either sketch a few points or use the fact that the graph is a parabola that opens downward to sketch the graph.
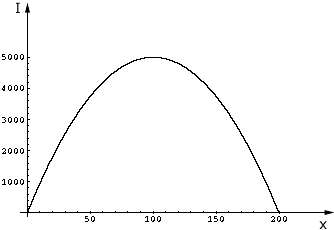
From the graph you can see the value of x that maximizes the income.
Penny