I am currently unable to find a proof that the diaonals of an isosceles trapezoid are congruent. Might you happen to have one?
Thanx,
Daniel
Daniel,
The key insight into all properties of the isosceles trapezoid is its symmetry. If you join the midpoints of the known parallel sides, then this line is a mirror of symmetry, In fact, this is the preferred (inclusive) definition of this class of quadrilaterals.
If you start with this symmetry, then it is clear that one diagonal goes to the other, under the reflection, and therefore they are the same length, and intersect on this mirror.
However, if you start with a different definition, you will need to do some additional proof to find the mirror.
For example, if you start with "two sides equal, two other sides parallel", then you need some additional information to make sure it is not a parallelogram. Basically, take the two parallel sides and one of the 'equal sides' of length r, with the side running from A to D. The other side, BC is typically not parallel to AD (unless we have two right angles - see below). In this case, the two sides BC and AD meet at a point P to make a triangle, with the final parallel side cutting this triangle parallel to the base. The only way the two segments AD and BC cut off by the parallel side can be equal is if the entire side AP and BP are also equal, as the parallel lines preserve ratios of segments being cut off. Given AP and BP are equal, we have a larger isosceles triangle which has a mirror of symmetry bisecting the angle at P and right bisecting the base AD. This is the desired mirror.
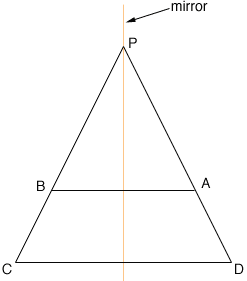
If you happen to start with a right angle at A, then the only possible equal side at B will also be the perpendicular (the shortest distance between the two lines). This immediately sets up the congruence of triangles ABC and BAD, using common side, angle and equal side (SAS). The congruence in question is reflection in the mirror mentioned above, and the third sides (now equal) are the diagonals.
There are a number of 'definitions' for Isosceles Trapezoids around. However, the optimum definitions are inclusive (yes a rectangle is an isosceles trapezoid) and do not use phrases such as: the equal sides are not parallel. That type of negative condition actually messes up the larger pattern of how these classes relate to one another - and mess up the logic when people reason.
Walter Whiteley