Quandaries and Queries
  

 

Hi my name is daniel, I am 14 and i have been given a piece of maths coursework whereby a farmer has to fence off a piece of land as large as possible using 1000m of fence. I already know that the formula for working out the area of any shape of a 1000m perimeter = 5002/ n*tan*(180/n), however, after some research I have found out that as the number of sides (n), tends to infinity, the n*tan*(180/n) tends to pi. Why is this? If you could e-mail me the answer it would be great.
 

 

Hi Daniel,

The key to this is the fact that,

if t is in radians then, as t tends to zero, sin(t)/t tends to 1.

I am not going to prove this for you, there is a proof in the Math Archives at the University of Tennessee in Knoxville Tennessee.

180 degrees is radians and hence 180/n degrees is /n radians. Hence, rewriting your expression with the angle expressed in radians rather than degrees gives

n tan(  /n )

Now let t = /n and you expression can again be rewritten, this time as

n tan(t) = n  sin(t)/coos(t)

But n =  /t and hence

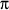
n  sin(t)/cos(t) =  /t  sin(t)/cos(t) =   sin(t)/t  1/cos(t)

Now, as n tends to infinity, t tends to zero and hence  sin(t)/t tends to 1 and cos(t) tends to 1. Thus your expression tends to

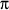
  1 1 =

Penny

  
 

Go to Math Central