Who is asking: Student
Level: Secondary
Question:
i was asked as a question in coursework to sketch the graph with the following characteristics:
a double root at -3
a pair of imaginary roots
an x-intercept at 6
a root at 4 which is not a double root
i also have to work out an equation that has the minimum possible degree for the properties to be simultaniously possible...
and im stuck!
Hi,
I am going to do a similar problem.
Sketch the graph of a polynomial with the following characteristics:
a double root at 2
a root at -1 which is not a double root
Since there is a simple root at -1 the graph crosses the x-axis at x = -1. In the graph below I chose to start the graph below the x-axis and cross to above the x-axis at -1.
The graph then has a double root at x = 2 so the graph comes back down to the x-axis and just touches it at x = 2, but doesn't cross the axis.
Below is a sketch of a graph that meets these conditions.
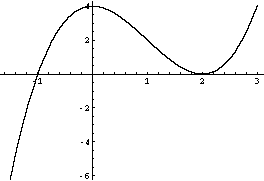
If you want an equation of a polynomial that meets these requirements then the equation must have a factor of (x+1) if it has a root at -1 and it must have a factor of (x-2)2 if it has a double root at 2. Since these ae the only conditions you have to satisify an equation with minimal degree would be
y = (x + 1)(x - 2)2
Suppose now that I change the problem slightly
Sketch the graph of a polynomial with the following characteristics:
a double root at 2
a root at -1 which is not a double root
a complex root
One way to introduce a complex root is to put a dip in the graph, between x = -1 and x = 2, but a shallow enough dip that it doesn't cross the x-axis.
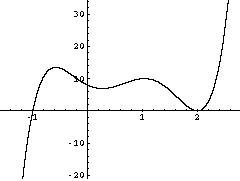
To introduce this dip into the equation you can add a factor that is a quadratic with complex roots. I did it by adding the factor
5 x2 - 2 x + 2
so the equation becomes
y = (x + 1)(x - 2)2 (5 x2 - 2 x + 2)
This actually has two complex roots since complex roots come in pairs.
Penny