Question:
I am trying to figure out how many square feet are in a piece of property. Start at Point A-then go 140 feet north-then 100 feet due east-then 300 feet at an angle southeast so that connecting to point A would be a straight line (right angle to first line north.)
I sure hope you can understand this description. I'd really appreciate it if you could tell me HOW you figure something like this.
Thanks.

Deb

Hi Deb,

I drew a diagram of you lot and added a perpendicular line from C to DA meeting DA at P to see that the lot can be divided into a rectangle APCB and a right triangle DCP.

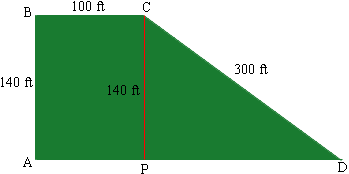
The rectangular section has area 100 140 = 14 000 square feet. The area of a triangle is half the base times the height so I can calculate the area of the triangle if I can find the length of the base PD. I can find this using Pythagoras' Theorem. (It is really amazing how useful this theorem is.)

Pythagoras' Theorem for triangle DCP says

|CP|² + |PD|² = |DC|²

That is

140² + |PD|² = 300²

so

|PD| = Sqrt[300² - 140²] = Sqrt[70400] = 265.33 ft

Hence the area of the triangle is

 ¹/₂ |PD| |CP| = ¹/₂ 265.33 140 = 18 573 square feet.

Thus the area of your property is

14 000 + 18 573 = 32 573 square feet.

Penny

Go to Math Central