I am building a wishing-well out of pieces of 2-by-4. I have included a picture of a miniature version of what I want. There are to be ten 2-by-4 pieces around the well and I want the circle around the outside of the structure to have a diameter of approximately 3 feet. How long to I cut the 2-by-4's to build the wishing-well.

Thanks,
Don

Hi Don,

Here is the photo you included.

I sketched a top-down view of the first row of 2-by-4's on a circular base of diameter 3 feet and labeled some points. (The diagram is not to scale.)

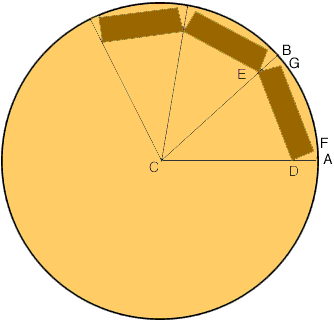
Since there are 10 pieces of 2-by-4 and the angle at the center of a circle is 360^o, the angle BCA is 36^o. Now bisect the angle BCA and extend the side GF of the 2-by-4 to meet the outside circle at A.

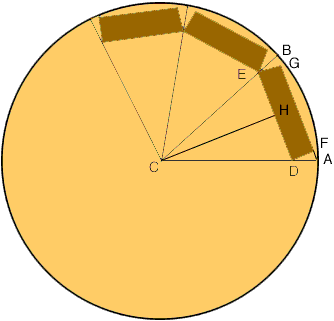
The line segments CH and DF are parallel and the angle HCD is 18^o, hence the angle FDA is 18^o. Angle DFA is a right angle and hence

cos( 18^o) = ^|FD|/_|DA| or |DA| = ^|FD|/_cos(18^o)

The width of a 2-by-4 is 3.5 inches so

|DA| = ^3.5/_0.9511 = 3.68 inches.

Thus |CD| = 18 - 3.68 = 14.32 inches.

Now look at triangle HCD. Angle HCD is 18^o, and

sin( 18^o) = ^|HD|/_|CD| so

|HD| = |CD| sin(18^o) = 14.32 3.309 = 4.43 inches.

Thus the length of the 2-by-4 is 2 4.43 = 8.83 inches. This is approximately 8 and ⁷/₈ inches.

Harley

Go to Math Central