Quandaries and Queries
  

 

Could you please help me with this question?

Problem: One corner of a 60X120 foot lot, otherwise rectangular, is a curve with a radius of 20 feet and a central angle of 90 degrees. What is the area?

Thanks for your consideration.

Sincerely,
EM
 

 

Hi,

I drew a diagram of what I think is the shape of the lot.

If this is the shape of the lot then I see it in four pieces, three rectangles and a quarter of a circular disk.

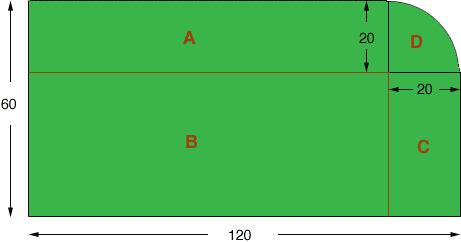
  1. The rectangle A is 100 feet by 20 feet and has area 2,000 square feet.
  2. The rectangle B is 100 feet by 40 feet and has area 4,000 square feet.
  3. The rectangle C is 40 feet by 20 feet and has area 800 square feet.
  4. The region D is a quarter of a circular disk of radius 20 feet. The arrea od a circle is 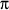times the radius squared so the area of D is 1/4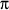 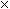  202 = 314.16 square feet.

The area of the lot is these sum of the four areas.

Penny

We received a follow-up question.

What happens when the central angle is lets say 50 degrees. I guess then we would calculate the area as of the arc as 1/7.2 r2.

Please advise.

You are correct that the area of a sector of a circle of radius r and central angle 50 degrees is 1/7.2 r2 but you need to take some care with the rest of the lot. In this situation I see the lot as divided into six regions, one of which is the sector, three are rectangles and two are congruent triangles.

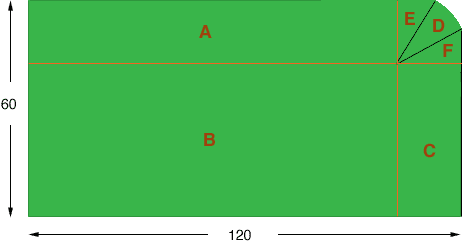
To calculate the area of the lot you need to know the lengths of the sides of the triangle F. I redrew and labeled the triangle F.

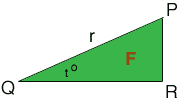
If the central angle of the sector D is 50 degrees the the angle t in the diagram is one half of 90 degrees minus 50 degrees which is 20 degrees. From this, and a knowledge of the radius r you can find the lengths of the two remaining sides of the triangle F.

sin(20o) = |PR|/r and cos(20o) = |QR|/r

thus

|PR| = r sin(20o) and |QR| = r cos(20o)

Now you can calculate the areas of the six regions that make up your lot. The area od D you know. You can use the expression "half the base times the height" to find the areas of E and F. The other three are rectangles. For example C has dimensions |QR| by 60 - |QR|.

Penny

  
 

Go to Math Central