Quandaries
and Queries
Suppose a set can be divided into a countably infinite number of countably infinite sets.Then can the original set be considered as a countably infinite set?
Hi Feroz,
Yes, the union of a countably infinite collection of countably infinite sets is countably infinite.
Arrange the elements of each of your countably infinite sets in a row.
| First set | |
|---|---|
| Second set | |
| Third set | |
Now create your large set by stacking each of the rows to form an array consisting of a countable infinite collection of countably infinite rows.
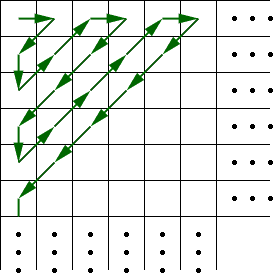
You can show this set is countably infinite by showing how to count its elements. This counting can be done by following the arrows in the diagram below.
Penny